Вся электронная библиотека >>>

Социально-экономическая статистика >>

 

Мультиколлинеарность

 

Одним из основных препятствий эффективного применения множественного регрессионного анализа является мультиколлинеарность. Она связана с линейной зависимостью между аргументами х₁, х₂, ..., х_k. В результате мультиколлинеарности матрица парных коэффициентов корреляции и матрица (X^TX) становятся слабообусловленными, т.е. их определители близки к нулю.

Это приводит к неустойчивости оценок коэффициентов регрессии (53.12), завышению дисперсии s, оценок этих коэффициентов (53.14), так как в их выражения входит обратная матрица (X^TX)^-1, получение которой связано с делением на определитель матрицы (Х^TХ). Отсюда следуют заниженные значения t(b_j). Кроме того, мультиколлинеарность приводит к завышению значения множественного коэффициента корреляции.

На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше 0,8, т.е. | r_jl | > 0,8, то считают, что имеет место мультиколлинеарность, и в уравнение регрессии следует включать один из показателей — х_j или x_l.

Чтобы избавиться от этого негативного явления, обычно используют алгоритм пошагового регрессионного анализа или строят уравнение регрессии на главных компонентах.

 

Пример. Построение регрессионного уравнения

 

Согласно данным двадцати (п = 20) сельскохозяйственных районов, требуется построить регрессионную модель урожайности на основе следующих показателей:

у — урожайность зерновых культур (ц/га);

x₁ — число колесных тракторов (приведенной мощности) на 100 га;

х₂ — число зерноуборочных комбайнов на 100 га;

х₃ — число орудий поверхностной обработки почвы на 100 га;

x₄ — количество удобрений, расходуемых на гектар;

 

 

 

 

х₅ — количество химических средств оздоровления растений, расходуемых на гектар.

Исходные данные для анализа приведены в табл. 53.1.

 

Таблица 53.1

Исходные данные для анализа

 

 

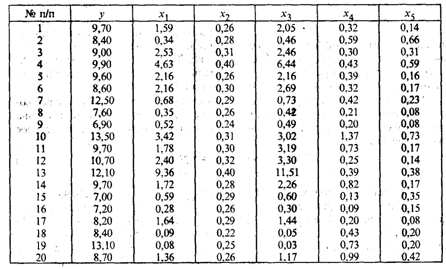
Решение. С целью предварительного анализа взаимосвязи показателей построена матрица R — таблица парных коэффициентов корреляции.

 

 

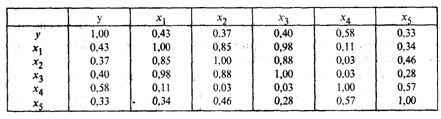
Анализ матрицы парных коэффициентов корреляции показывает, что результативный признак наиболее тесно связан с показателем х₄ — количеством удобрений, расходуемых на гектар (r_yx4 = 0,58).

В то же время связь между аргументами достаточно тесная. Так, существует практически функциональная связь между числом колесных тракторов (x₁) и числом орудий поверхностной обработки почвы x₃(r_x1x3) = 0,98.

О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции r_x1x2 = 0,85 и r_x3x2 = 0,88.

Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим рассчитанное на ЭВМ регрессионное уравнение урожайности, включив в него все исходные показатели:

 

 = 3,515 – 0,006x₁ + 15,542x₂ + 110x₃ + 4,475х₄ - 2,932x_5.                            (53.22)

                                               (-0,01)       (0,72)        (0,13)    (2,90)     (-0,95)

 

В скобках указаны t_набл (β_j) = t_j — расчетные значения t-критерия для проверки гипотезы о значимости коэффициента регрессии Н₀: β_j = 0, j = 1, 2, 3, 4, 5. Критическое значение t_кр = 1,76 найдено по таблице t-распределения при уровне значимости α = 0,1 и числе степеней свободы v = 14. Из уравнения следует, что статистически значимым является коэффициент регрессии только при х₄, так как |t₄| = 2,90 > t_кр = 1,76. Не поддаются экономической интерпретации отрицательные значения коэффициентов регрессии при х₁ и x₅, из чего следует, что повышение насыщенности сельского хозяйства колесными тракторами (х₁) и средствами оздоровления растений (x₅) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо.

После реализации алгоритма пошагового регрессионного анализа с исключением переменных и учетом того, что в уравнение должна войти только одна из трех тесно связанных переменных (x₁, х₂ или x₃), получаем окончательное уравнение регрессии

 

 = 7,342 + 0,345x₁ + 3,294x₄.                    (53.23)

                                                             (11,12)   (2,09)       (3,02)

 

Уравнение значимо при α = 0,05, так как F_набл = 266 > F_кр = 3,20, найденного по таблице F-распределения при α = 0,05, v₁ = 3 и v₂ = 17. Значимы и коэффициенты регрессии β₁ и β₄, так как |t_j| > t_кр = 2,11 (при α = 0,05, v = 17). Коэффициент регрессии β₁ следует признать значимым (β₁ ≠ 0) из экономических соображений; при этом t₁ = 2,09 лишь незначительно меньше t_кр = 2,11. В случае если α = 0,1, t_кр = 1,74 и коэффициент регрессии β₁ статистически значим.

Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни приводит к росту урожайности зерновых в среднем на 0,345 ц/га (b₁ = 0,345).

Коэффициенты эластичности Э₁ = 0,068 и Э₄ = 0,161 (Э_j = ) показывают, что при увеличении показателей x₁ и х₄ на 1% урожайность зерновых повышается соответственно на 0,068% и 0,161%.

Множественный коэффициент детерминации r = 0,469 свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедними в модель показателями (x₁ и x₄), т.е. насыщенностью растениеводства тракторами и  удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (х₂, x₃, х₅, погодными условиями и др.). Средняя относительная ошибка аппроксимации  = 10,5% свидетельствует об адекватности модели, так же как и величина остаточной дисперсии s² = 1,97.

 

К содержанию книги: Курс социально-экономической статистики

 

Смотрите также:

  

 СТАТИСТИКА ЭКОНОМИЧЕСКАЯ. Отрасль статистики, изучающая ...

СТАТИСТИКА ЭКОНОМИЧЕСКАЯ. Отрасль статистики, изучающая материальное производство с целью выявления пропорций, тенденций и закономерностей развития ... bibliotekar.ru/biznes-15-6/133.htm

 

  ПРОГНОЗ ЭКОНОМИЧЕСКОЙ АКТИВНОСТИ статистика ...

ПРОГНОЗ ЭКОНОМИЧЕСКОЙ АКТИВНОСТИ ... Вводный курс по экономической теории ... Главные направления современной экономической bibliotekar.ru/biznes-64/164.htm

 

  Деньги. Кредит. Банки

Л.П. Кроливецкой. - М.: Финансы и статистика, 1996. Березина М.П. Безналичные расчеты в экономике России. - М.: Консалт-банкир, 1997. bibliotekar.ru/biznes-36/index.htm

 

  ОСНОВНЫЕ ВИДЫ ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ

ОСНОВНЫЕ ВИДЫ ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ ... Статистика дает общую картину состояния и развития национального хозяйства, освещает ... bibliotekar.ru/mezhdunarodnye-otnosheniya.../184.htm

 

  Моделирование рисковых ситуаций в экономике и бизнесе

Для студентов, обучающихся по специальностям «Статистика», « Математические методы и исследование операций в экономике», « bibliotekar.ru/riskovye-situacii-2/index.htm

 

  Практическое значение экономической теории. Главные ...

межотраслевых (экономическая география, демография, статистика и др.). Экономическая теория — одна из общественных наук наряду с историей, ... bibliotekar.ru/biznes-38/9.htm

 

  Принципы экономической науки

Азимов Л.Б., Журавская Е.В., Макарова О.Ю. Преподавание экономики в школе. ... М.: Финансы и статистика, 1994. ... Антология экономической bibliotekar.ru/biznes-63/25.htm

 

  Деятельность предприятия. Экономика предприятия

М.: Финансы и статистика, 1996. 11. Настольная книга финансиста / Под ред. В.Г. Панскова. – М: Международный центр финансово-экономического ... www.bibliotekar.ru/economika-predpriyatiya/

 

ВНЕШНЕЭКОНОМИЧЕСКИЕ СВЯЗИ   Внешнеэкономическая деятельность предприятия